In western music an octave is devided into 12 equal steps.
The frequencies form a geometric sequence with factor
2 1/12 . This multiplicative structure comes from the fact
that the human ear listens logarithmically. Rational Frequency relations are
considered "harmonic" . A geometric sequence is translational
invariant but can only approximate rational numbers. With 12 steps, this
can be achieved well, better for example than in Stockhausen's
5 1/5 scale.
Euler's music theory assigns to a frequency ratio
p/q a number G(p,q)=G(p/q) called "gradus suavitatis" which could
be translated as "degree of pleasure". G(p/q) is defined as
1+ sum ei (p i-1), where p i are the prime
factors with multiplicity ei of the least common multiple of p and q.
Lets look at the little decime 12/5=p/q.
Since lcm(12,5)= 60=22+3+5, we have
G(12/5) = (1+ 2*1+1*(3-1)+1*(5-1)) = 9
The geometric scale with 12 steps interpolating the frequency doubling 1:2 allows to approximate
some rational numbers "with pleasure". For example,
2 2/12 = 1.122462048 ... is close to 9/8=1.125.
The function G(n,m) can be determined with the
online-calculator to the left (look at the source to see the implementation in Javascript).
Here is a Mathematica implementation of the Gradus Suavitatis:
G[p_,q_]:=Module[{s=FactorInteger[LCM[p,q]/GCD[p,q]]},1+Sum[s[[k,2]]*(s[[k,1]]-1),{k,Length[s]}]]
which was used to plot the function G(n,m) on the positive quadrant
in the integer plane. The color encodes the value of G(n,m).
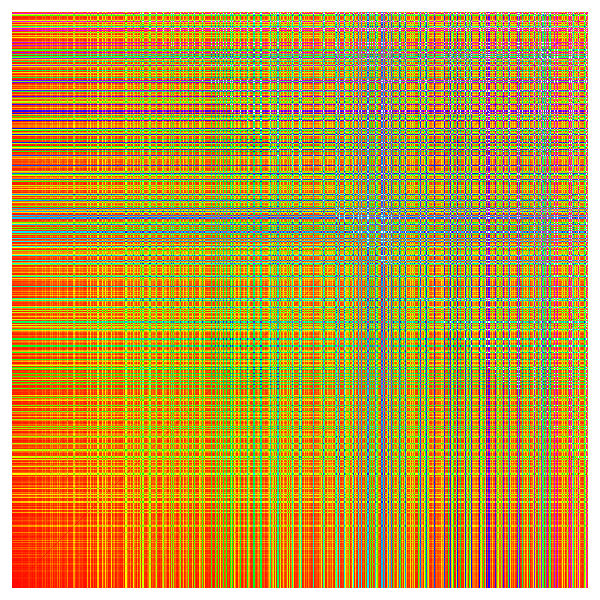
larger poster,
smaller poster.
|
|
References:
Wille: Mathematische Musiktheorie, 1983 [PDF],
in "Musik and Mathematik" (in german), editors Heinz Götze and Rudolf Wille, Springer.
Acknowledgements:
|