All triangles are equilateral

All triangles are equilateral (click on picture to continue)

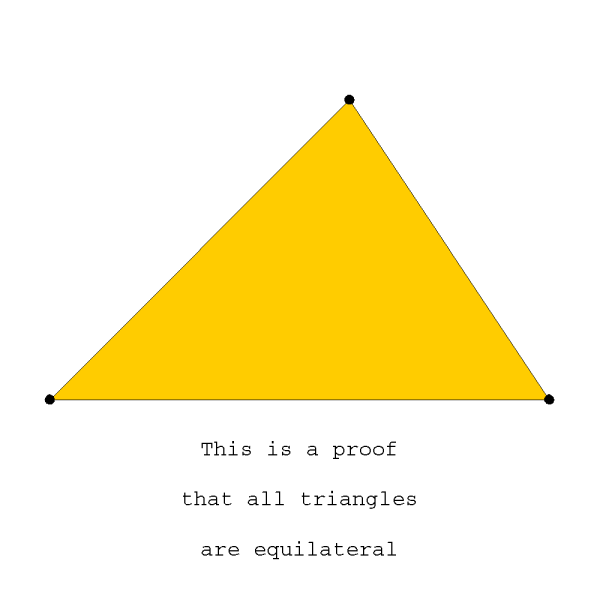
This mindboggling proof shows that all triangles are equilateral. It is quite old I learned around 1985 as student at ETH. The proof can be found in Volume 3 of Morris Klines "Mathematical Thoughts from Ancient to Modern Times" (p. 1006). The proof is interesting for computer scientists working on algorithms which can verify mathematical proofs. If you go throught the above arguments, there is no error in the argumentation. All steps are ok. But still something is wrong. What?
Once you see it, you will realize an important source for potential flaws in mathematical arguments.

Reader comment submitted on April 28, 2006: "The instruction start with a line that bisects the angle at C, but in your example that line doesn't divide the angle in two equal angles, so it does't really bisects the angle C. How can you say that the argumentation has no error if that same argumentation is based on a drawing that doesn't follow the intructions?"

Answer: We look at a mathematical proof, not a geometric construction. So, just assume that the angle has been bisected and use the consequences in the proof. The error in the argumentation chain is not quantitative, it is more fundamental.